Banach bundle (non-commutative geometry)

In mathematics, a Banach bundle is a fiber bundle over a topological Hausdorff space, such that each fiber has the structure of a Banach space.

Definition

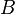Let X be a topological Hausdorff space, a (continuous) Banach bundle over X is a tuple \mathfrak{B} = (B, \pi), where B is a topological Hausdorff space, and \pi\colon B\to X is a continuous, open surjection, such that each fiber B_x := \pi^{-1}(x) is a Banach space. Which satisfies the following conditions:

  1. The map b\mapsto\|b\| is continuous for all b\in B
  2. The operation +\colon\{(b_1,b_2)\in B\times B:\pi(b_1)=\pi(b_2)\}\to B is continuous
  3. For every \lambda\in\mathbb{C}, the map b\mapsto\lambda\cdot b is continuous
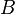  4. If x\in X, and \{b_i\} is a net in B, such that \|b_i\|\to 0 and \pi(b_i)\to x, then b_i\to 0_x\in B. Where 0_x denotes the zero of the fiber B_x.[1]

If the map b\mapsto \|b\| is only upper semi-continuous, \mathfrak{B} is called upper semi-continuous bundle.

Examples

Trivial bundle

Let A be a Banach space, X be a topological Hausdorff space. Define B := A\times X and \pi\colon B\to X by \pi(a,x) := x. Then (B,\pi) is a Banach bundle, called the trivial bundle

See also

References

  1. ↑ Fell, M.G., Doran, R.S.: "Representations of *-Algebras, Locally Compact Groups, and Banach *-Algebraic Bundles, Vol. 1"
This article is issued from Wikipedia - version of the 1/9/2013. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.