Graph amalgamation
In graph theory, a graph amalgamation is a relationship between two graphs (one graph is an amalgamation of another). Similar relationships include subgraphs and minors. Amalgamations can provide a way to reduce a graph to a simpler graph while keeping certain structure intact. The amalgamation can then be used to study properties of the original graph in an easier to understand context. Applications include embeddings,[1] computing genus distribution,[2] and Hamiltonian decompositions.
Definition
Let  and
and 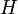 be two graphs with the same number of edges where
be two graphs with the same number of edges where  has more vertices than
has more vertices than 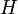 . Then we say that
. Then we say that 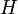 is an amalgamation of
is an amalgamation of  if there is a bijection
if there is a bijection  and a surjection
and a surjection  and the following hold:
and the following hold:
- If
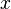 ,
, 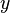 are two vertices in
are two vertices in  where
where  , and both
, and both 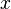 and
and 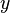 are adjacent by edge
are adjacent by edge  in
in  , then
, then  and
and  are adjacent by edge
are adjacent by edge  in
in 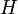 .
. - If
 is a loop on a vertex
is a loop on a vertex  , then
, then  is a loop on
is a loop on  .
. - If
 joins
joins  , where
, where  , but
, but  , then
, then  is a loop on
is a loop on  .[3]
.[3]
Note that while  can be a graph or a pseudograph, it will usually be the case that
can be a graph or a pseudograph, it will usually be the case that 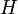 is a pseudograph.
is a pseudograph.
Properties
Edge colorings are invariant to amalgamation. This is obvious, as all of the edges between the two graphs are in bijection with each other. However, what may not be obvious, is that if  is a complete graph of the form
is a complete graph of the form  , and we color the edges as to specify a Hamiltonian decomposition (a decomposition into Hamiltonian paths, then those edges also form a Hamiltonian Decomposition in
, and we color the edges as to specify a Hamiltonian decomposition (a decomposition into Hamiltonian paths, then those edges also form a Hamiltonian Decomposition in 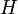 .
.
Example

Figure 1 illustrates an amalgamation of  . The invariance of edge coloring and Hamiltonian Decomposition can be seen clearly. The function
. The invariance of edge coloring and Hamiltonian Decomposition can be seen clearly. The function 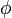 is a bijection and is given as letters in the figure. The function
is a bijection and is given as letters in the figure. The function 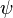 is given in the table below.
is given in the table below.
 |  |
|---|---|
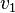 |  |
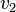 |  |
 | 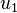 |
 |  |
 |  |
Hamiltonian decompositions
One of the ways in which amalgamations can be used is to find Hamiltonian Decompositions of complete graphs with 2n + 1 vertices.[4] The idea is to take a graph and produce an amalgamation of it which is edge colored in 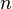 colors and satisfies certain properties (called an outline Hamiltonian decomposition). We can then 'reverse' the amalgamation and we are left with
colors and satisfies certain properties (called an outline Hamiltonian decomposition). We can then 'reverse' the amalgamation and we are left with  colored in a Hamiltonian Decomposition.
colored in a Hamiltonian Decomposition.
In [3] Hilton outlines a method for doing this, as well as a method for finding all Hamiltonian Decompositions without repetition. The methods rely on a theorem he provides which states (roughly) that if we have an outline Hamiltonian decomposition, we could have arrived at it by first starting with a Hamiltonian decomposition of the complete graph and then finding an amalgamation for it.
Notes
References
- Bahmanian, Amin; Rodger, Chris (2012), "What Are Graph Amalgamations?", Auburn University
- Hilton, A. J. W (1984), "Hamiltonian Decompositions of Complete Graphs, Journal of Combinatorial Theory, Series B 36, 125–134
- Gross, Jonathan L.; Tucker, Thomas W. (1987), Topological Graph Theory, Courier Dover Publications, 151
- Gross, Jonathan L. (2011), "Genus Distributions of Cubic Outerplanar Graphs", Journal of Graph Algorithms and Applications, Vol. 15, no. 2, pp. 295–316