Logical hexagon

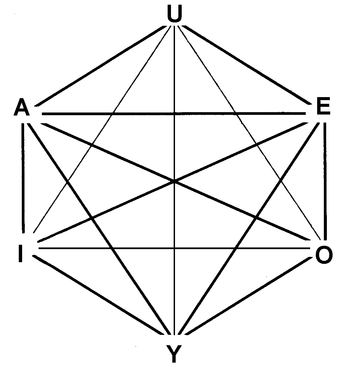
The logical hexagon extends the square of opposition to six statements.

The logical hexagon (also called the hexagon of opposition) is a conceptual model of the relationships between the truth values of six statements. It is an extension of Aristotle's square of opposition. It was discovered independently by both Augustin Sesmat and Robert Blanché.[1]

This extension consists in introducing two statements U and Y. Whereas U is the disjunction of A and E, Y is the conjunction of the two traditional particulars I and O.

Summary of relationships

The traditional square of opposition demonstrates two sets of contradictories A and O, and E and I (i.e. they cannot both be true and cannot both be false), two contraries A and E (i.e. they can both be false, but cannot both be true), and two subcontraries I and O (i.e. they can both be true, but cannot both be false) according to Aristotle’s definitions. However, the logical hexagon provides that U and Y are also contradictory.

Interpretations of the logical hexagon

The logical hexagon may be interpreted in various ways, including as a model of traditional logic, quantifications, modal logic, order theory, or paraconsistent logic.

The statement A may be interpreted as "Every man is white."

(∀x)(Mx → Wx) ∧ (∃x)(Mx)

The statement E may be interpreted as "Every man is non-white."

(∀x)(Mx → ¬Wx)

The statement I may be interpreted as "Some man is white."

(∃x)(Mx ∧ Wx)

The statement O may be interpreted as "Not every man is white."

(∃x)(Mx ∧ ¬Wx) ∨ ¬(∃x)(Mx)

The statement U may be interpreted as "Either every man is white or every man is non-white."

(∀x)(Mx → Wx) ∨ (∀x)(Mx → ¬Wx)

The statement Y may be interpreted as "Some man is white and some man is non-white"

(∃x)(Mx ∧ Wx) ∧ (∃x)(Mx ∧ ¬Wx)

Modal logic

The logical hexagon may be interpreted as a model of modal logic such that

Further extension

It has been proven that both the square and the hexagon, followed by a “logical cube”, belong to a regular series of n-dimensional objects called “logical bi-simplexes of dimension n.” The pattern also goes even beyond this.[2]

See also

References

  1. ↑ N-opposition theory logical hexagon
  2. ↑ Moretti, Pellissier

Further reading

This article is issued from Wikipedia - version of the 1/3/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.