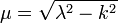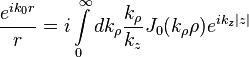Sommerfeld identity

The Sommerfeld identity is a mathematical identity, due Arnold Sommerfeld, used in the theory of propagation of waves,

\frac{{e^{ik R} }} {R} = \int\limits_0^\infty I_0(\lambda r) e^{ - \mu \left| z \right| } \frac{{\lambda d \lambda}}{{\mu}}

where

\mu = \sqrt {\lambda ^2 - k^2 }

is to be taken with positive real part, to ensure the convergence of the integral and its vanishing in the limit 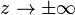$z \rightarrow \pm \infty$ and

R^2=r^2+z^2

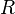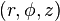Here, $R$ is the distance from the origin while $r$ is the distance from the central axis of a cylinder as in the $(r,\phi,z)$ cylindrical coordinate system. Here the notation for Bessel functions follows the German convention, to be consistent with the original notation used by Sommerfeld. The function 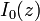$I_0(z)$ is the zeroth-order Bessel function of the first kind, better known by the notation 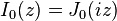$I_0(z)=J_0(iz)$ in English literature. This identity is known as the Sommerfeld Identity [Ref.1,Pg.242].

In alternative notation, the Sommerfeld identity can be more easily seen as an expansion of a spherical wave in terms of cylindrically-symmetric waves,

\frac{{e^{ik_0 r} }} {r} = i\int\limits_0^\infty {dk_\rho \frac{{k_\rho }} {{k_z }}J_0 (k_\rho \rho )e^{ik_z \left| z \right|} }

Where

k_z=(k_0^2-k_\rho^2)^{1/2}

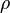[Ref.2,Pg.66]. The notation used here is different form that above: $r$ is now the distance from the origin and $\rho$ is the radial distance in a cylindrical coordinate system defined as 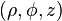$(\rho,\phi,z)$ . The physical interpretation is that a spherical wave can be expanded into a summation of cylindrical waves in 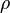$\rho$ direction, multiplied by a two-sided plane wave in the 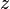$z$ direction; see the Jacobi-Anger expansion. The summation has to be taken over all the wavenumbers $k_\rho$ .

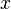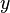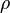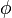The Sommerfeld identity is closely related to the two-dimensional Fourier transform with cylindrical symmetry, i.e., the Hankel transform. It is found by transforming the spherical wave along the in-plane coordinates ( $x$ , $y$ , or $\rho$ , $\phi$ ) but not transforming along the height coordinate $z$ .

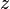References

Sommerfeld, A.,Partial Differential Equations in Physics,Academic Press,New York,1964
Chew, W.C.,Waves and Fields in Inhomogeneous Media,Van Nostrand Reinhold,New York,1990

This article is issued from Wikipedia - version of the 2/24/2016. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.