Uniform absolute continuity

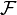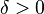In mathematical analysis, a collection $\mathcal{F}$ of real-valued and integrable functions is uniformly absolutely continuous, if for every $\epsilon > 0$ , there exists $\delta>0$ such that for any measurable set 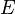$E$ , $\mu(E)<\delta$ implies

\int_E \!|f|\, \mathrm{d}\mu < \epsilon

for all $f\in \mathcal{F}$ .

References

J. J. Benedetto (1976). Real Variable and Integration - section 3.3, p. 89. B. G. Teubner, Stuttgart. ISBN 3-519-02209-5
C. W. Burrill (1972). Measure, Integration, and Probability - section 9-5, p. 180. McGraw-Hill. ISBN 0-07-009223-0

This article is issued from Wikipedia - version of the 11/7/2014. The text is available under the Creative Commons Attribution/Share Alike but additional terms may apply for the media files.

Uniform absolute continuity

See also

References